动态规划解最长公共子序列(LCS)-参考资料
https://blog.csdn.net/zhaoluwei/article/details/52193985
LCS填表过程-参考资料
https://blog.csdn.net/weixin_40673608/article/details/...
概念
子序列形式化定义:
给定一个序列X=,另一个序列Z=,若存在一个严格递增的X的下标序列对所有的1,2,3,…,k,都满足x(ik)=zk,则称Z是X的子序列。
比如Z=是X=的子序列
公共子序列定义:
如果Z既是X的子序列,又是Y的子序列,则称Z为X和Y的公共子序列。
最长公共子序列(以下简称LCS):
2个序列的子序列中长度最长的那个。
蛮力法求解最长公共子序列:
需要遍历出所有的可能,时间复杂度是O(n³),太慢了。
动态规划求解最长公共子序列:
分析规律:
设X=,Y=为两个序列,Z=是他们的任意公共子序列。
经过分析,我们可以知道:
1、如果xm = yn,则zk = xm = yn 且 Zk-1是Xm-1和Yn-1的一个LCS
2、如果xm != yn 且 zk != xm,则Z是Xm-1和Y的一个LCS
3、如果xm != yn 且 zk != yn,则Z是X和Yn-1的一个LCS
所以如果用一个二维数组c表示字符串X和Y中对应的前i,前j个字符的LCS的长度话,可以得到以下公式:

意思是:
设
p1表示X的前 i-1 个字符和Y的前 j 个字符的LCS的长度;
p2表示X的前 i 个字符和Y的前 j-1 个字符的LCS的长度;
p表示X的前 i-1 个字符和Y的前 j-1 个字符的LCS的长度;
p0表示X的前 i 个字符和Y的前 j 个字符的LCS的长度;
如果X的第 i 个字符和Y的第 j 个字符相等,则p0 = p + 1;
如果X的第 i 个字符和Y的第 j 个字符不相等,则p0 = max(p1,p2)。
做法:
因此,我们只需要从c[0][0]开始填表,填到c[m-1][n-1],所得到的c[m-1][n-1]就是LCS的长度。
但是,我们怎么得到LCS本身而非LCS的长度呢?
也是用一个二维数组b来表示:
在对应字符相等的时候,用↖标记;
在p1 >= p2的时候,用↑标记;
在p1 < p2的时候,用←标记。
伪代码:

若想得到LCS,则再遍历一次b数组就好了,从最后一个位置开始往前遍历:
如果箭头是↖,则代表这个字符是LCS的一员,存下来后 i-- , j--
如果箭头是←,则代表这个字符不是LCS的一员,j--
如果箭头是↑ ,也代表这个字符不是LCS的一员,i--
如此直到i = 0或者j = 0时停止,最后存下来的字符就是所有的LCS字符
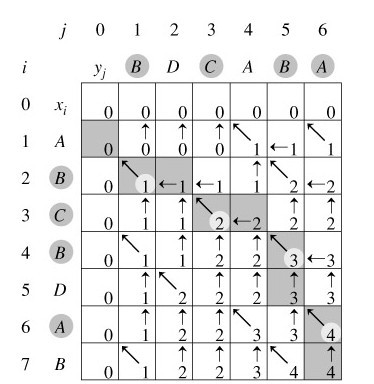
比如说求ABCBDAB和BDCABA的LCS:
C++代码实现:
字符串长度上限支持自定义,可直接输出LCS表和箭头表以及最优解。
// 博主原创,请勿直接使用在作业中
#include <iostream>
using namespace std;
void getLCS_Length();
string getLCS();
const int subStringLengthA = 12;
const int subStringLengthB = 12; // 支持的最长字符串的有效字符数, 自行设置
const char LEFTUP = '`'; // means"左上方"
const char UP = '^'; // means"上方"
const char LEFT = '<'; // means"左方"
int lens[subStringLengthA + 1][subStringLengthB + 1] = {0}; // 记录子问题x[i]和y[i]的LCSLength
char marks[subStringLengthA + 1][subStringLengthB + 1] = {0}; // 方向标记
string A, B;
int main() {
int tmp_len;
cin >> A;
cin >> B;
A = string(1, ' ').append(A.substr(0, A.size() + 1)); // A[0]=' ', A[1...]有效
B = string(1, ' ').append(B.substr(0, B.size() + 1)); // B[0]=' ', B[1...]有效
tmp_len = (int)A.size();
if(tmp_len < subStringLengthA + 1)
for(int i = 0; i < subStringLengthA - tmp_len; i++)
A = A.append(string(1, 'w')); // 长度不足则以该缺省值补充
tmp_len = (int)B.size();
if(tmp_len < subStringLengthB + 1)
for(int i = 0; i < subStringLengthB - tmp_len; i++)
B = B.append(string(1, 'w'));
for(int i = 0; i <= subStringLengthA; i++)
for(int j = 0; j <= subStringLengthB; j++)
marks[i][j] = '*';
getLCS_Length();
cout << "lens[i][j]:" << endl;
for(int i = 0; i <= subStringLengthA; i++){
for(int j = 0; j <= subStringLengthB; j++)
cout << lens[i][j] << ' ';
cout << endl;
}
cout << "marks[i][j]:" << endl;
for(int i = 0; i <= subStringLengthA; i++){
for(int j = 0; j <= subStringLengthB; j++)
cout << marks[i][j] << ' ';
cout << endl;
}
cout << "LCS:" << endl << getLCS() << endl;
return 0;
}
void getLCS_Length(){
int m = subStringLengthA;
int n = subStringLengthB;
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
if(A[i] == B[j]){
lens[i][j] = lens[i - 1][j - 1] + 1;
marks[i][j] = LEFTUP;
}else if(lens[i - 1][j] >= lens[i][j - 1]){
lens[i][j] = lens[i - 1][j];
marks[i][j] = UP;
}else{
lens[i][j] = lens[i][j - 1];
marks[i][j] = LEFT;
}
}
string getLCS(){
string ans;
int m = subStringLengthA;
int n = subStringLengthB;
while(m > 0 && n > 0) {
switch (marks[m][n]) {
case LEFTUP:
ans.append(string(1, A[m]));
m--;
n--;
break;
case UP:
m--;
break;
case LEFT:
n--;
break;
default:
break;
}
}
reverse(ans.begin(), ans.end());
return ans;
}









Comments NOTHING